Если даны два вектора a и b, задача «длина вектора a + 3b» решается двумя простыми способами: через координаты и через скалярное произведение. Ниже — коротко и наглядно.
Шаг 1. Устанавливаем и запускаем программу
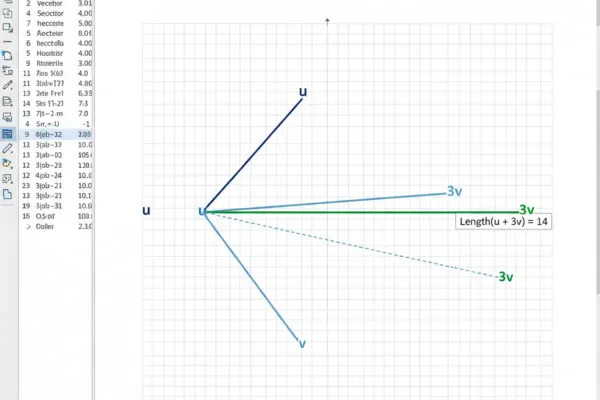
Для быстрого вычисления и проверки можно использовать GeoGebra — введите в поле ввода векторы и получайте длину моментально. Также подойдёт любой графический калькулятор или онлайн-сервис.
Шаг 2. Осваиваем основной сценарий
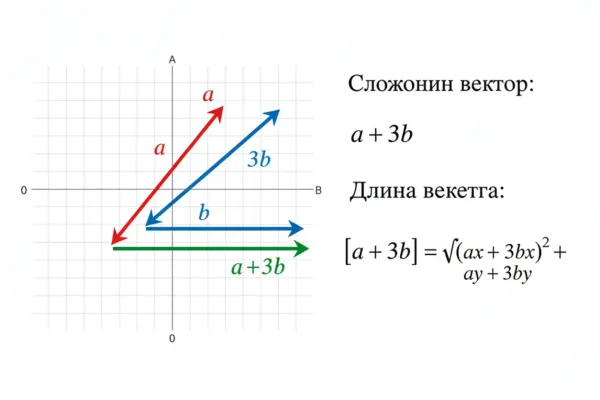
- Если заданы координаты: a=(ax,ay,az), b=(bx,by,bz), вычислите c = a + 3b = (ax+3bx, ay+3by, az+3bz). Потом |c| = sqrt((ax+3bx)^2 + (ay+3by)^2 + (az+3bz)^2).
- Если известны длины и скалярное произведение: используйте формулу
|a + 3b|^2 = |a|^2 + 2*3*(a·b) + 9|b|^2 = |a|^2 + 6(a·b) + 9|b|^2
и затем берёте квадратный корень. - Пример: a=(1,2), b=(3,1). Тогда a+3b=(1+9,2+3)=(10,5), |a+3b|=sqrt(100+25)=sqrt(125)=5√5.
Шаг 3. Полезные функции и советы
- Если не хотите развернуть формулы вручную — в GeoGebra введите векторные переменные и команду Norm(a+3b) или просто вычислите компоненты и используйте sqrt(...).
- При отсутствии координат используйте скалярное произведение: a·b=|a||b|cosφ — это удобно, когда известны углы между векторами.
- Проверяйте знак: для выражения a - 3b формула меняется на |a - 3b|^2 = |a|^2 - 6(a·b) + 9|b|^2.
Чем усилить работу с вычислениями
- GeoGebra — интерактивная среда для векторов и формул.
- Desmos — графический калькулятор для быстрых вычислений и визуализации (онлайн).
- WolframAlpha — решатель выражений и векторных задач (онлайн).
Коротко: если у вас координаты — просто сложите компоненты и найдите модуль; если нет — примените формулу через скалярное произведение. GeoGebra удобно проверит расчёт и покажет результат наглядно.
Полезные ссылки
- GeoGebra — интерактивная среда для работы с векторами и графиками
- Desmos — графический калькулятор (онлайн)
- WolframAlpha — онлайн‑решатель математических выражений