Коротко: покажу, как в GeoGebra быстро вычислить длину вектора a+3b — удобно, когда есть координаты векторов. Подойдёт для задач по геометрии и физике.
Шаг 1. Устанавливаем и запускаем программу
Скачайте и откройте GeoGebra (есть десктоп и веб‑версия). Для быстрых вычислений достаточно веб‑версии: откройте калькулятор или окно «Геометрия».
Шаг 2. Осваиваем основной сценарий
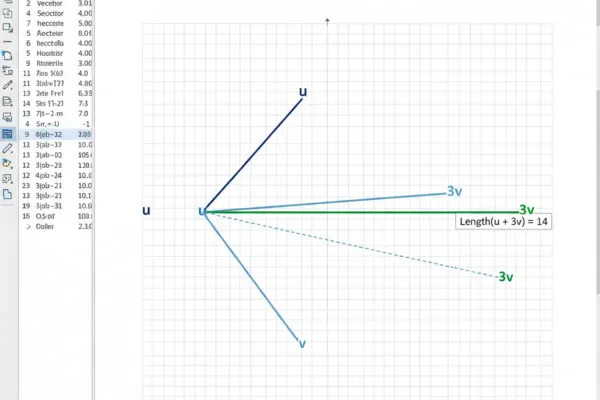
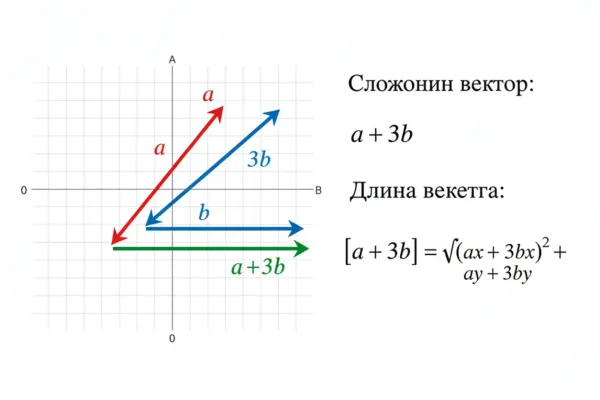
Если заданы координаты векторов a=(ax,ay) и b=(bx,by), длина вектора a+3b считается по стандартной формуле. В GeoGebra сделайте так:
- Вставьте координаты: введите A=(ax, ay) и B=(bx, by), либо сразу вектор a=(ax,ay) и b=(bx,by).
- Создайте комбинированный вектор: в поле ввода напишите v = a + 3*b.
- Найдите длину: введите Length(v) или используйте команду Norm[v]. Результат — скаляр с длиной в тех же единицах, что и координаты.
Шаг 3. Полезные функции и советы
- Если у вас трёхмерные векторы, GeoGebra поддерживает 3D: используйте объекты в виде (x,y,z) и ту же команду Length.
- Можно не вводить точки: прямо в поле ввода напишите Length((ax,ay) + 3*(bx,by)).
- Проверяйте промежуточно компоненты вектора: введите x(v) и y(v) или используйте команду Coordinates[v], чтобы увидеть сумму по координатам.
Чем усилить работу с GeoGebra
- GeoGebra — основной инструмент для вычислений и визуализации.
- Desmos — удобный графический калькулятор для визуализации в 2D и проверки результатов.
- WolframAlpha — подойдёт для проверки формул и получения пошагового решения по векторам.
Итого: для длины a+3b достаточно координат векторов; GeoGebra даёт быстрый ввод и команду Length, а Desmos и WolframAlpha пригодятся для визуальной проверки и пошаговой проверки решений.